Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y=ax2 donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio, y se bosquejará a continuación usando notación moderna.
Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea V un punto en el eje y sea QV perpendicular al eje. (QV corresponde al valor x en la versión analítica y PV al valor y). Considerando la sección circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y C.

Por el teorema de potencia de un punto:
Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:.
Usando nuevamente los paralelismos:.
Despejando HV y VK para sustituir en la fórmula de QV² resulta en.
Pero el valor de.

es una constante pues no depende de la posición de V, por lo que haciendo
arroja la expresión moderna y=ax².
Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.
La ecuación de una parábola cuyo eje es vertical y su vértice es (u,v) tiene la forma (y-v)=a(x-u)2, |
agrupando los términos y reordenando se obtiene una forma equivalente:
La ecuación de una parábola cuyo eje es vertical es de la forma |
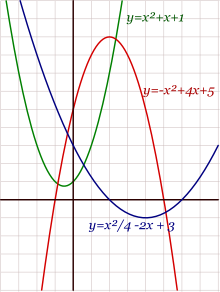
Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por x y viceversa. Así tendríamos:
La ecuación de una parábola cuyo eje es horizontal es de la forma |
La ecuación de una parábola cuyo eje es horizontal es de la forma
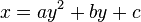 .
.

 .
.